Explain Different Types of Symmetry in Fem With Example

Using equation 312 we are now able to express and derivatives of the shape function in. Using Symmetry To Reduce FEA Runtime3.

Modelling Techniques Finite Element Method Part 2

All elements can be linear or quadratic the second.

. Note this is always a plane but in 2D problems it will be seen as a line as the 3rd direction you dont have in 2D is also the second direction of the symmetry plane. This element is quite useful when symmetry with respect to geometry and loading exists about an axis of the body being analyzed. Define the element types to be used Chapter 6.

Create Material with properties defined above E 210000 MPa and ν 03 2. Boundary conditions are the conditions at the surfaces of a body. The finite element mesh is used to specify the geometry of the solid and is also used to describe the displacement field within the solid.

Depending on the physical situation some terms may be dropped-Boundary conditions 1. Meshing for the Finite Element Method. The finite element method FEM is a popular method for numerically solving differential equations arising in engineering and mathematical modeling.

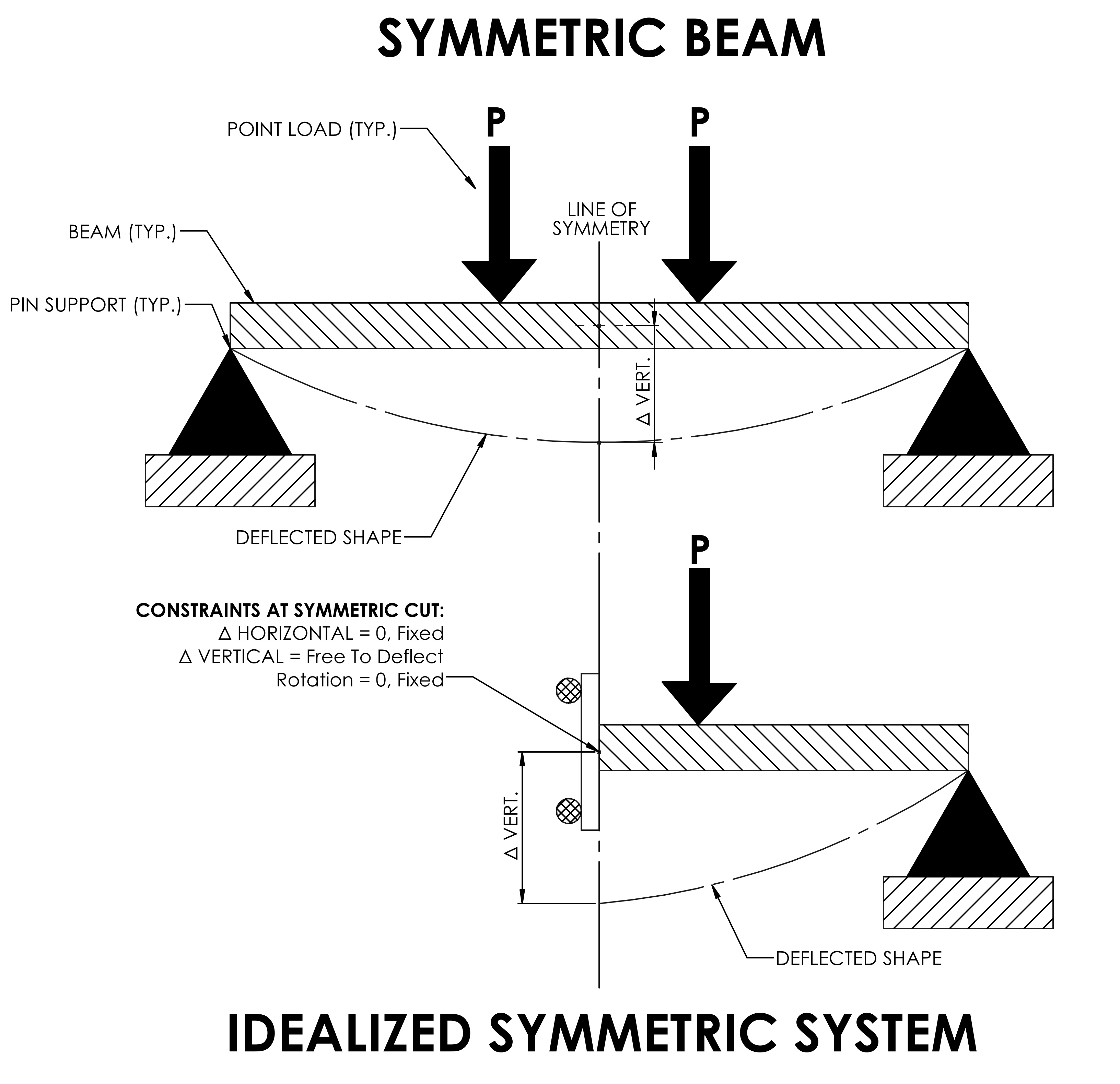
Find the symmetry plane. Define the geometric proper ties of the elements length area and the like. Typical problem areas of interest include the traditional fields of structural analysis heat transfer fluid flow mass transport and electromagnetic potential.

CIVL 78117 Chapter 9 - Axisymmetric Elements 166. An example is given in Fig 1 of a Pin which must fit in the bored hole on the Block as. There are several types of Finite Elements.

Of FEM and surface integral equation on the boundary is generally referred to as FEM-BEM. Using Symmetry To Reduce FEA Runtime. Different terms in the governing equation can be identified with conduction convection generation and storage.

We will expand the unknown potential as a linear combination of basis functions so that r XN n1 anfnr 846. Create a 2D property of plate Thickness 1 mm 3. These are problems which are governed by differential equations and have to.

Reflection Symmetry sometimes called Line Symmetry or Mirror Symmetry is easy to see because one half is the reflection of the other half. Right Triangle One of the angles is 90 degrees. Equilateral Triangle All three sides and angles are equal.

A recent project spawned a water-cooler discussion regarding symmetry theory and FEA. Here my dog Flame has her face made perfectly symmetrical with a bit of photo magic. Describing function method in control system.

Define the material pr operties of the elements. In most types of control systems we can not avoid the presence of certain types of non-linearities. It is quite helpful to remember that finite element method is essentially a numerical method to solve certain kind of differential equations called boundary value problems.

Problems that involve soil masses subjected to circular footing loads or thick-walled pressure vessels can often be analyzed using the element developed in this chapter. The white line down the center is the Line of Symmetry also called the Mirror Line. Analytical Theoretical Comparison.

Initial conditions are the conditions at time t 0. The two methods are written below and briefly discussed with the help of an example. Here is the simple analysis process to solve this problem.

These can be classified as static or dynamic. The technology and computational efficiency of the method together with the rapid increases in computer processing power means that today the scope and size of simulations far exceeds the capabilities of even a few years ago. Line of symmetry may or may not be present.

Line of symmetry is present. 1 CHAP 4 FINITE ELEMENT ANALYSIS OF BEAMS AND FRAMES 2 INTRODUCTION We learned Direct Stiffness Method in Chapter 2 Limited to simple elements such as 1D bars we will learn Energy Methodto build beam finite element Structure is in. Enclosed in a frame with different letters used to identify each datum.

FEA is a powerful technique able to produce solutions to challenging structural analysis problems. For example theres a fast algorithm to nd a random point hidden in one of 1000000 elements that will take on average 500 trials rather than 500000 but it requires being able to move from one triangle to its neighbor. Define the physical constraints boundar y conditions.

Define the element connecti vities mesh the model. Datums When the base of the triangle lies on the outline or extension of the outline of a. A finite element mesh may be three dimensional like the example shown.

For convenience we will use the method of weighted residuals instead of the Rayleigh-Ritz approach. A typical mesh generated in the commercial FEA code ABAQUS is shown in the picture to the right. Scalene Triangle Length of all sides is unequal and all three angles have varying values.

You can use beamsplatessolids depending on your model. So lets take a look at various elements types used in FEA. Line of symmetry is present.

Just follow these steps. To use different order shape functions for unknown approximation and coordinate transformation known as sub-parametric or super-parametric formulation. Feature of a Component.

I developed a worked example using ANSYS LSDYNA to show underlying symmetry concepts manual application and advantages to symmetric analysis. Phase plane method in control system. With platessolids you can use easier to mesh triangular elements TRITET or more robust quadratic elements QUADHEX.

Answer 1 of 6.

Taking Advantage Of Symmetry In Fea Msc Nastran Simulating Reality Delivering Certainty

Using Symmetry To Reduce Fea Runtime

Modelling Techniques Finite Element Method Part 2